Z축에 대한 회전 공식 (+유도 과정)

directX를 이용해 라이브러리를 개발하던 중

z 축을 기준으로 회전하는 공식을 유도한 과정이다.

이 평면좌표 위의 두 선을

이 위치로 옮겼다 생각하자

좌표 두 개를 각각 (x, y), (x', y')라고 정해주면

알 수 있는 사실은 다음과 같다.

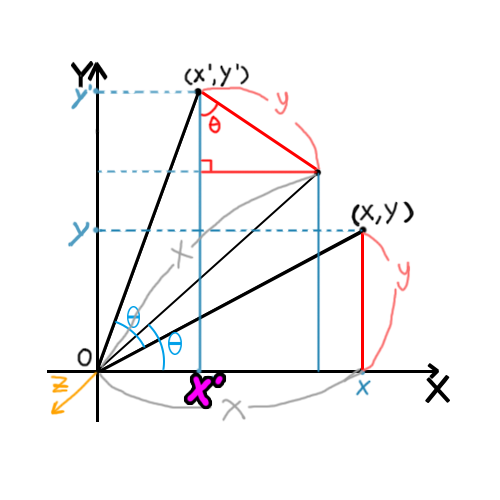
먼저 x'를 구해보자.

 

 x' = xcosθ - ysinθ 

y'를 구해보자

 y' = xsinθ + ycosθ 

구한 식은 행렬로 나타낼 수 있다.

(수학에서의 행렬은 연립방정식을 풀기 위해 사용되지만 cpu graphics에서의 행렬은  변환의 목적으로 쓰인다.)

 

행렬은 인풋값과 아웃풋 값이 같아야 계산 가능하다.

그렇기에 나는 저 행렬을 3by 3 행렬로 인풋 값에 z값까지 받아오게끔 변형시켰다.

(당연히 아웃풋도 z'까지 나온다.)

 

[ X' ]      [ cosθ   -sinθ   0 ] [ x ]

| y  |  =  | sinθ    cosθ    0 | | y |

[ z' ]      [   0      0      1   ] [ z ]

 

이런 식으로,,

 

참고로 Scale, Translate, Rotation의 각각 행렬을 보면,

이렇게 나타나 지는데 ST행렬은 아래와 같이 표현될 수 있다.

이렇듯 2차원을 translate 하면 3차원이 되고 3dmax 등에서는 3차원에서 한번 더 평행 이동함으로써 4차원 행렬을 사용한다. (4 by 4)

--------------------------------------------------------------------------

 

Y = TRX와 Y = RTX 

 

두 식은 확연히 다르니 주의해서 구현하도록 하자!